| С.Вавилов и К.Ермоленко. Стохастические системы управления портфелем ценных бумаг | ||
| Re: Портфельные стратегии -- admin3 | Ответить | Форум |
|
Отправлено: 07/17/2003, 18:34:57 |
Стохастические системы управления портфелем ценных бумаг Нестабильность современных финансовых рынков заставляет пересмотреть многие традиционные схемы управления капиталом, базирующиеся как на фундаментальном и техническом анализе, так и на бурно развивающейся на Западе в последнее десятилетие теории известной под названием "money management" ([1]). Дело в том, что основополагающим для упомянутой выше теории "money management" , является фактическое предположение, часто формулируемое в неявном или завуалированном виде, о стационарном характере функции распределения, определяющей вероятность выигрыша или проигрыша в каждой отдельно взятой парной (полностью обнуляющей позиции) сделке при использовании той или иной торговой стратегии. Естественно, что в современных условиях такое предположение начинает выглядеть весьма проблематичным. Таким образом, возникает естественное стремление, оставив в силе основную идею современной теории управления капиталом (для достижения приемлемой доходности, по возможности, экономно использовать предоставляемый финансовый ресурс), построить схему управления, не использующую в явном или неявном виде указанное предположение. Роль подобных схем управления могут играть стохастические системы. Принципиальным внешним отличием стохастической системы от привычных схем управления капиталом является, как правило, непарность совершаемых сделок, а именно, от открытия до закрытия позиции система может покупать и частично продавать различное количество акций, оставаясь при этом в рамках заданных бюджетных ограничений. Главенствующим условием применения данной схемы управления капиталом является не первоначальный объем инвестированных средств, а наличие, пусть относительно небольшого, но непрерывного денежного потока, например, из общего потока поступающих прибылей инвестора, обеспечивающего диверсификацию общего бизнеса и направляемого на конкретный финансовый сегмент рынка. При достижении приемлемого уровня доходности дополнительные денежные средства, обеспечившие наряду с первоначальным объемом инвестированных средств, ее реализацию, могут по необходимости либо реинвестироваться, либо направляться на другие сегменты. Таким образом, гибкое маневрирование денежными потоками является основой успешного применения указанной схемы управления инвестиционным портфелем. Однако, даже приостановка в силу ряда причин необходимой денежной подкачки в систему управления, первоначально занимающую длинную позицию (бумаги не заимствуются), вовсе не означает прекращение спекуляций по достижению приемлемого уровня доходности на общий объем вложенных денежных средств. В этой ситуации на другом субсчете, позволяющем избежать клиринговых сделок, начинают совершаться "короткие продажи" (short sales) на основе системы управления, занимающей короткую позицию, под залог уже приобретенных акций. Таким образом, в стохастической системе управления отсутствует традиционное понятие "stop loss", означающее фиксирование убытков при достижении ими определенного заранее установленного уровня. Указанные системы не стараются "угадать" направление движения рынка, а обеспечивают "продавливание" средневзвешенной цены совершаемых сделок вниз или вверх, в зависимости от использования системы управления занимающей длинную или короткую позицию. Основой успешного функционирования указанной системы управления является не движение цены акций вверх или вниз, а наличие их высокой ликвидности и внутри дневной волатильности, которые в силу высокой спекулятивности современного финансового рынка имеют тенденцию к росту. В настоящей статье обсуждается применяемая на практике простейшая стратегия управления портфелем, включающем один вид ценных бумаг и наличные деньги, базирующаяся лишь на весьма общих предположениях о стохастическом характере процесса ценообразования и обеспечивающая, при выполнении ряда, как правило, реально имеющих место условий относительно динамики цены и достаточном финансовом ресурсе, приемлемый асимптотический во времени рост прибыли. Более сложная стратегия управления портфелем, включающем несколько видов ценных бумаг и наличные деньги, требует отдельного рассмотрения. Первоначально опишем систему управления, занимающую только длинную позицию. Введем в рассмотрение понятие стоимости портфеля
где
Зададим торговую стратегию, определяющую на каждый момент времени количество бумаг в портфеле, следующей зависимостью
Построение управляющей функции
где Напомним, что хорошо известной стратегии самофинансирования ([2]), соответствует зависимость (2), в которой Теоретической основой для конструирования стохастических систем управления портфелем является формулируемое ниже утверждение ([4]). Пусть выполняются следующие условия:
где Путь утверждения заключается в том, что при выполнении условий 1–4 можно построить управление портфелем, обеспечивающее асимптотический во времени рост капитала, при этом существенно отметить, что само управление Доказательство сформулированного утверждения базируется на приводимых ниже рассуждениях. Применяя к функции
Для удобства вычислений, без потери общности и с использованием соответствующей нормировки, вытекающей из второго предположения, будем полагать, что значения Введем в рассмотрение
Управление
Таким образом,
Кроме того, зададим следующие граничные условия
В силу соотношения (6) выполнение граничного условия (11) означает, что система управления стремится полностью избавиться от бумаг, если цена приближается к верхнему порогу чувствительности. Одновременно, из соотношения (1) видно что в силу граничного условия (12), система управления стремится купить бумаги на все имеющиеся в портфеле наличные деньги при стремлении цены к нижнему порогу чувствительности. Записывая решение смешанной задачи (10), (11), (12) для уравнения (5), где
при этом
Отметим, что в соотношениях (13), (14) используется явный вид решения задачи (7), (8) ([5]), при этом выбор первого собственного числа обеспечивает отличие от нуля соответствующей собственной функции внутри указанной полосы. Вводя в рассмотрение новую управляющую функцию
и используя зависимость (3), непосредственно получим формулу, определяющую изменение стоимости капитала вдоль наблюдаемого значения цены
Если управление Кроме того, исходя из формулы (6), нетрудно определить количество бумаг, которое необходимо иметь в портфеле при наблюдаемом значении цены
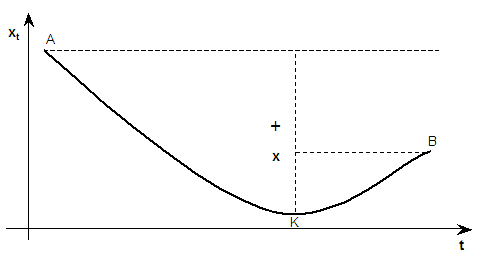
Заметим, что в соотношение (17) не входит не только В случае необходимости, изменяя границы указанной выше полосы, будем исходить из того, что наблюдаемое значение цены может находиться в некоторой произвольно малой, но конечной окрестности нижнего порога чувствительности лишь ограниченное время. Заметим, что аналогично можно сконструировать систему управления, занимающую только короткую позицию, при этом нужно лишь во втором условии сформулированного утверждения заменить требование отделимости "снизу" на требование отделимости "сверху". Указанные системы управление обладают следующим важным свойством. Первоначально рассмотрим вариант, когда используется только длинная позиция. На рис.1 пунктиром изображен некоторый ценовой уровень, относительно которого цена движется вниз, начиная с точки A, достигает дна образующейся ямки (точка K) и начинает двигаться вверх, достигая точки B, соответствующей средневзвешенной цене имеющихся в портфеле ценных бумаг (отдельные пакеты бумаг приобретаются по разным ценам в соответствии с формулой (17)), приобретенных на рассматриваемом ценовом интервале. Неравномерность объемов покупаемых/продаваемых пакетов ценных бумаг при реализации указанной системы управления всегда будет приводить к тому, что точка B располагается строго ниже середины глубины получившейся ямки, как указано на рис.1. Соответственно, система управления, занимающая только длинную позицию, увеличивает капитал при движении цены вверх, вбок и при не слишком сильном ее движении вниз, что означает существование относительно сильных "откатов" цены вверх. В случае системы, занимающей только короткую позицию, ситуация является зеркально противоположной и, соответственно, рост капитала происходит при движении цены вниз, вбок и при не слишком сильном ее движении вверх, что означает существование относительно сильных "откатов" цены вниз. Понятно, что для практического применения наиболее проблематичными из приведенных выше условий 1–4 являются первое и четвертое, а также процедура дискретизации, поскольку исходная система управления является непрерывной. Остановимся на данных вопросах более подробно.
Рис.1 Случай системы, занимающей длинную позицию. + – середина глубины ценовой ямки x – значение средневзвешенной ценыЧто касается первого предположения, то указанная система позволяет строить теоретическую кривую изменения стоимости капитала Относительно параметра дискретизации, когда система управления реагирует на определенное изменение цены, можно сказать, что данная величина определяется характерным локальным масштабом ее внутридневных колебаний и составляет на современных рынках величину порядка 1.5% – 2% от текущего значения цены. Что касается четвертого условия, то оно предполагает в случае достаточно резкого "безоткатного" изменения цены "подкачку" в портфель необходимого количества денежных средств для продолжения спекуляций. Разумеется, что на время использования дополнительных средств, общая доходность в процентах годовых исчисляется с их учетом. В случае достижения приемлемой доходности система управления, фиксируя прибыль, закрывает позиции, а дополнительно используемые денежные средства выводятся из оборота. Таблица 1. Итоговый протокол работы системы управления
Таблица 1. (продолжение)
В таблице 1 приведены итоговые результаты работы построенной системы управления, занимающую как длинную, так и короткую позицию, за определенные отрезки времени по ряду ценных бумаг, торгуемых как на американском NASDAQ, так и на российской ММВБ. При этом денежные средства исчисляются соответственно в долларах и рублях, а размер комиссионных на NASDAQ составляет 15 долларов за сделку, на ММВБ – 0.14% от оборота. Все приведенные расчеты сделаны без учета капитализации первоначального объема вложенных средств. Отметим, что фактическая доходность может существенно превышать задаваемую по причине скачкообразного изменения цены, особенно между торговыми сессиями.
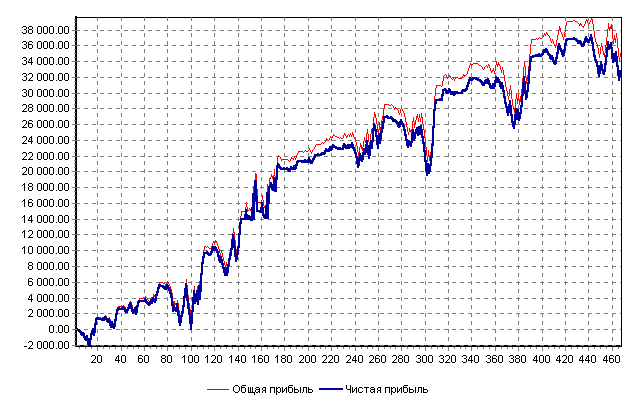
Рис. 2 Динамика изменения прибыли с использованием системы управления, занимающей длинную позицию, при спекуляциях акциями компании РАО "ЕЭС России" с 3.01.2002 по 2.10.2002. На рисунках 2, 3 приведена динамика изменения величины общей и чистой (с учетом комиссионных издержек) прибыли при использовании систем управления, занимающих соответственно длинную и короткую позиции, для спекуляций по акциям компании РАО "ЕЭС России" из таблицы 1. По оси абсцисс откладываются номера совершаемых сделок. Соответственно, график изменения цен совершаемых сделок по акциям указанной компании за соответствующий период времени изображен на рисунке 4. Наконец, в таблице 2 приведена выдержка из промежуточного протокола работы системы управления, занимающей длинную позицию при спекуляциях акциями Dell Computers Corporation из таблицы 1.
Рис. 3 Динамика изменения прибыли с использованием системы управления, занимающей короткую позицию, при спекуляциях акциями компании РАО "ЕЭС России" с 3.01.2002 по 2.10.2002.
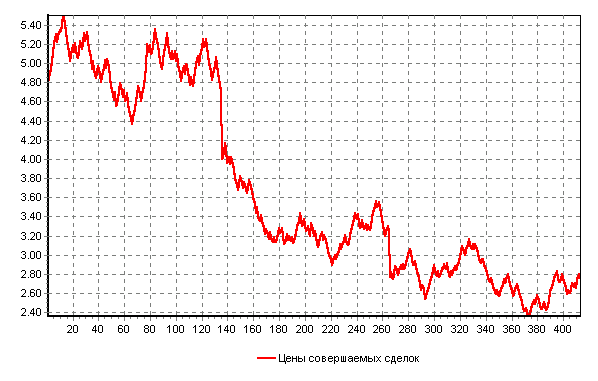
Рис. 4 График изменения цен совершаемых сделок по акциям компании РАО "ЕЭС России" за период с 3.01.2002 по 2.10.2002.
Таблица 2. Выдержка из промежуточного протокола торгов акциями компании Dell Corporation
Практическая реализация стохастических систем управления осуществляется с использованием ECN (электронных коммуникационных сетей), обеспечивающих оперативный доступ в режиме реального времени участникам фондового рынка к международным биржевым площадкам таким, как NASDAQ и NYSE с помощью различных систем прямого доступа ([6]). Доступ к торгам на ММВБ осуществляется с помощью информационно-торговой системы QUIK. Программное обеспечение работы стохастических систем управления реализуется через специальный программный комплекс Online Trader, описание которого будет дано в отдельной статье. 1. Ральф Винс Математика управления капиталом. Методы анализа рынка для трейдеров и портфельных менеджеров. Издательский дом Альпина, М., 2000. 2. W.H. Fleming, R.W. Rishel Deterministic and Stochastic Optimal Control, New York, Springer-Verlag, 1975. 3. М.Х.А. Дэвис Линейное оценивание и стохастическое управление. – М.: Наука, 1984. 4. S.A. Vavilov On the probability models to control the investor portfolio. In the book: Asymptotic methods in probability and statistics with applications, Birkhauser, Boston-Basel-Berlin, 2001, pp. 535-546. 5. Э. Камке Справочник по обыкновенным дифференциальным уравнениям. – М.: Наука, 1971. 6. Торговые системы прямого доступа. Сравнение и перспективы. "Современный трейдинг". №2, 2001 г. |
| Ответить | Назад |Вперед |Текущая страница |
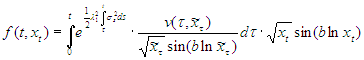 , (13)
, (13)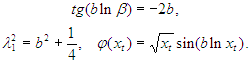 (14)
(14)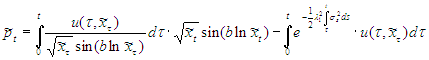 . (16)
. (16) . (17)
. (17)